The Marching Cubes algorithm is one of the most valuable algorithms in data visualization. To tackle its implementation, we need general data structures for 3D maths and precomputed lookup tables to avoid computations on the fly. Let’s assume, we have some scalar field representing data that we need to visualize. This could be a mathematical function generating a field, or a data obtained from CT, MR, and SPECT devices.
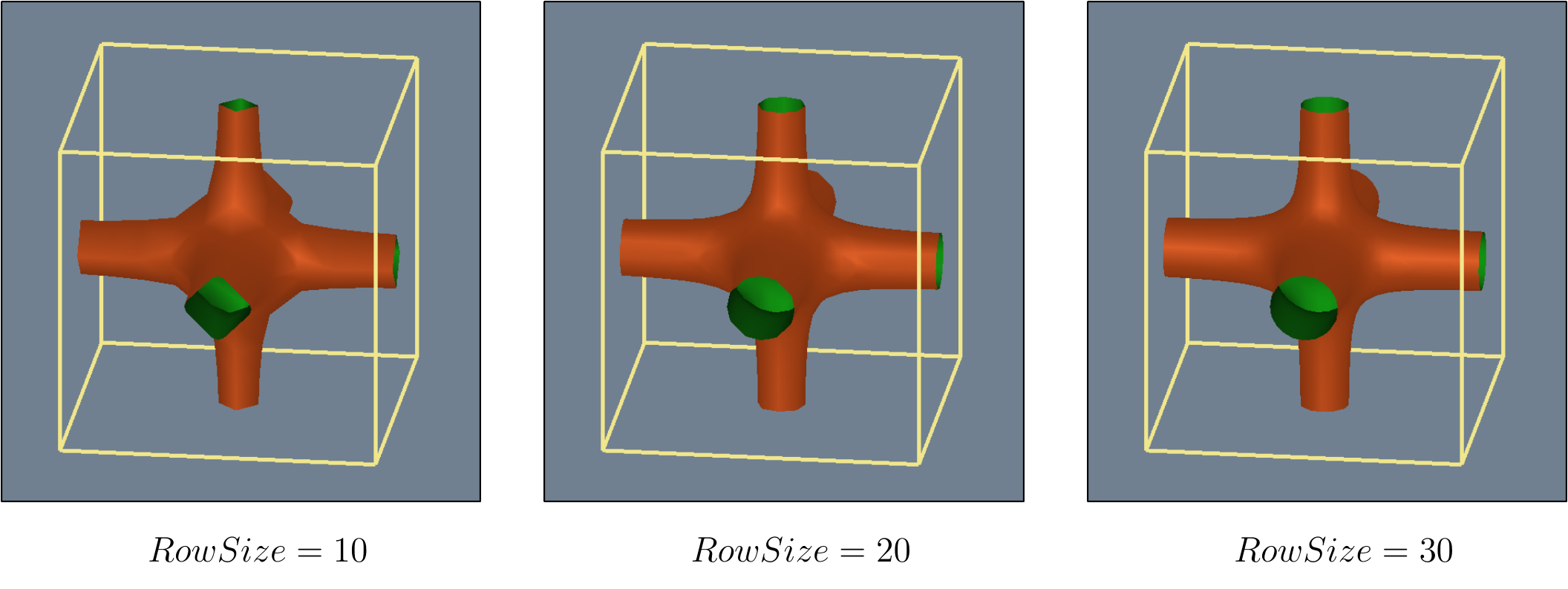
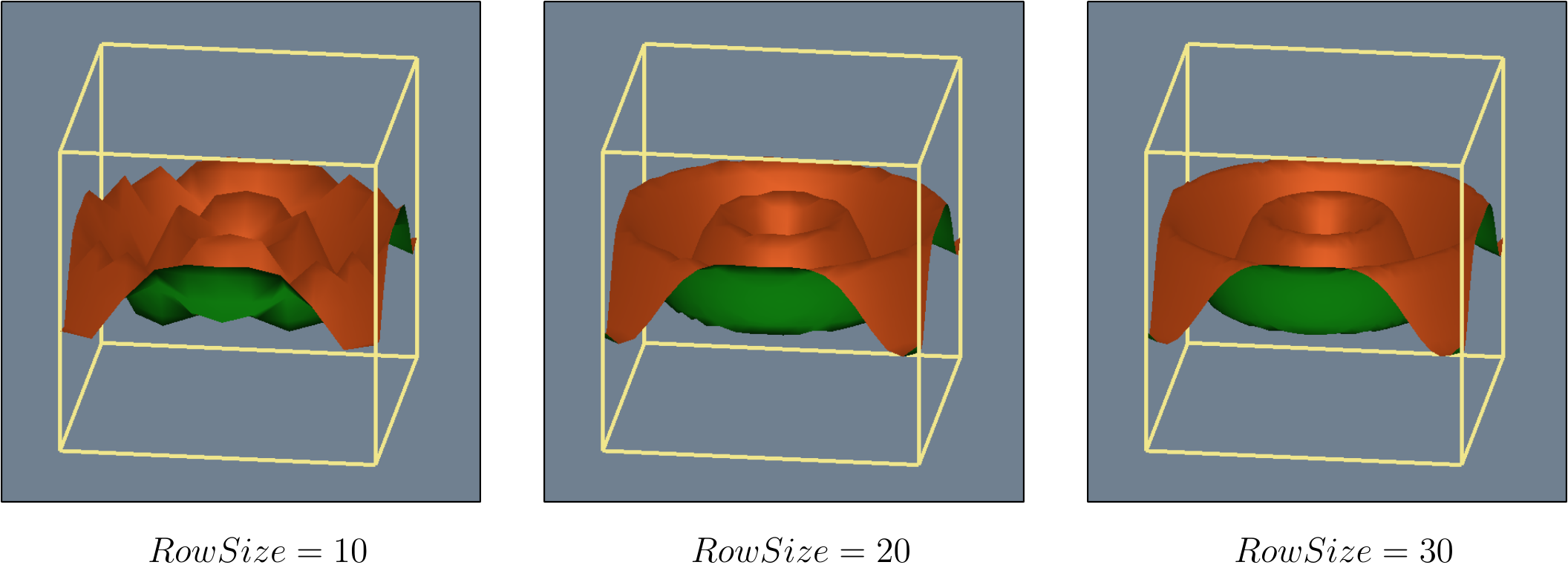
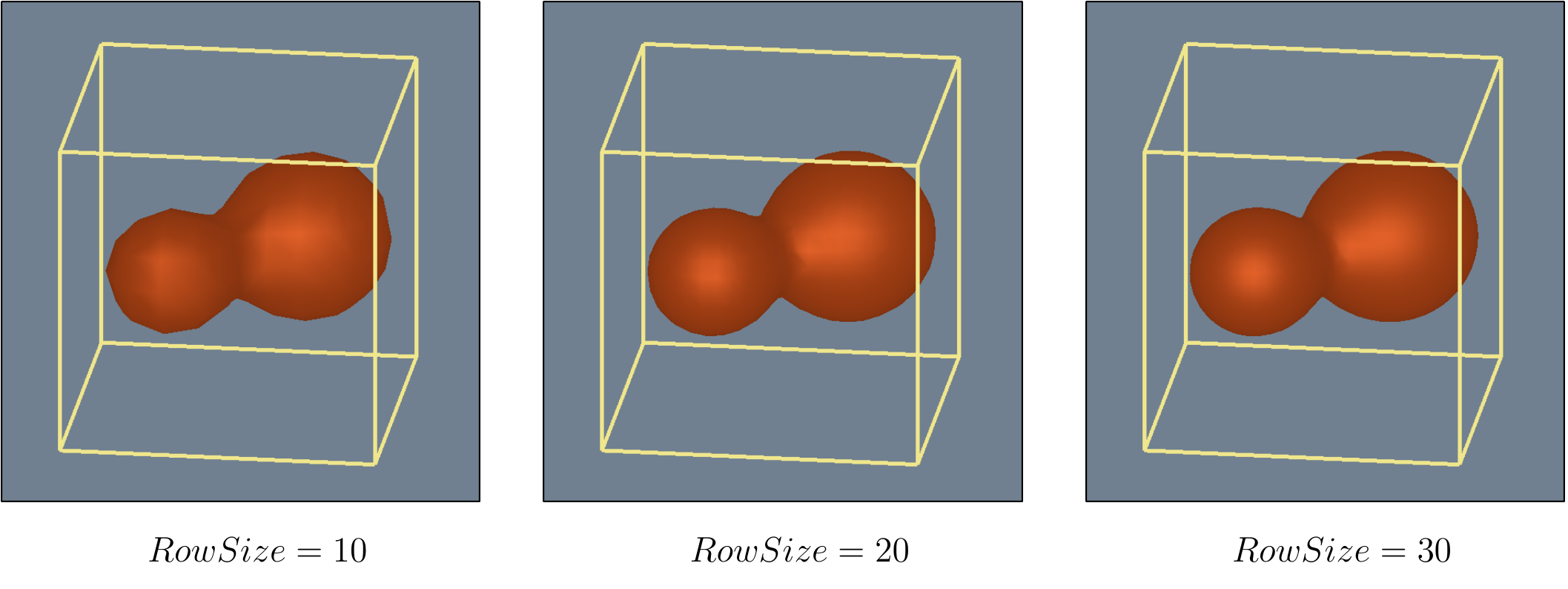
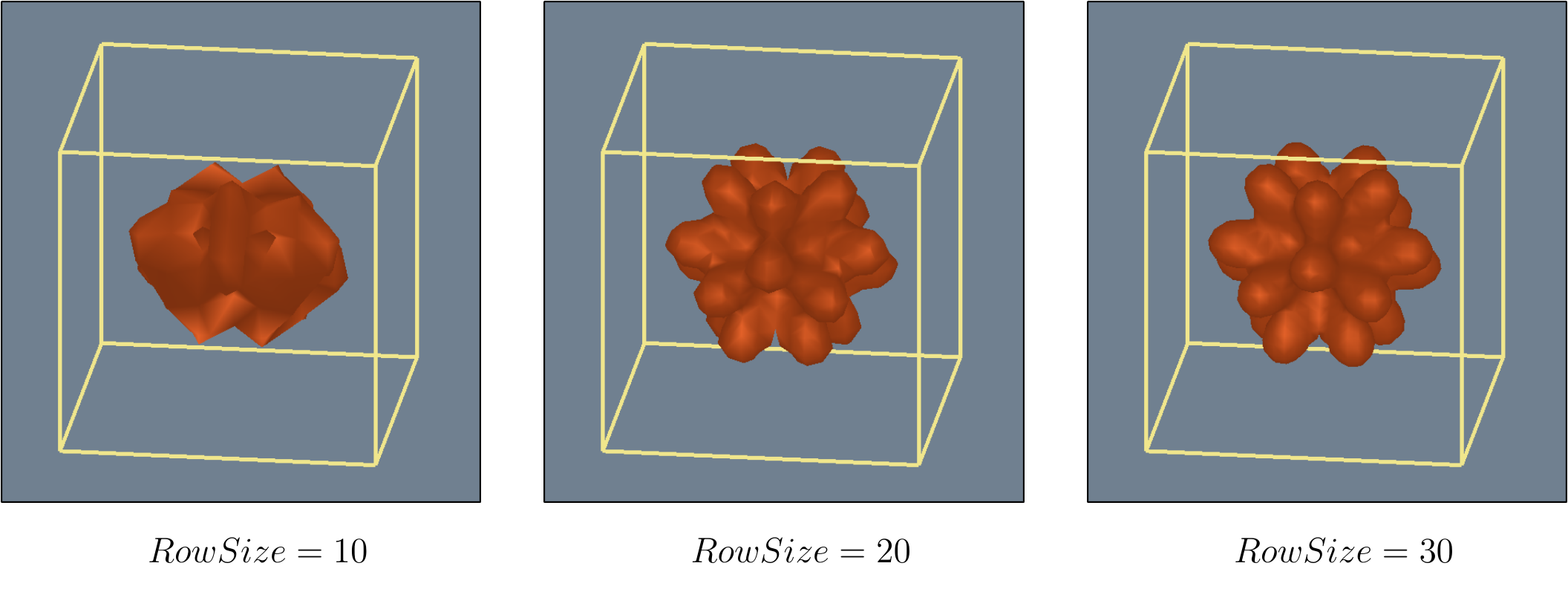
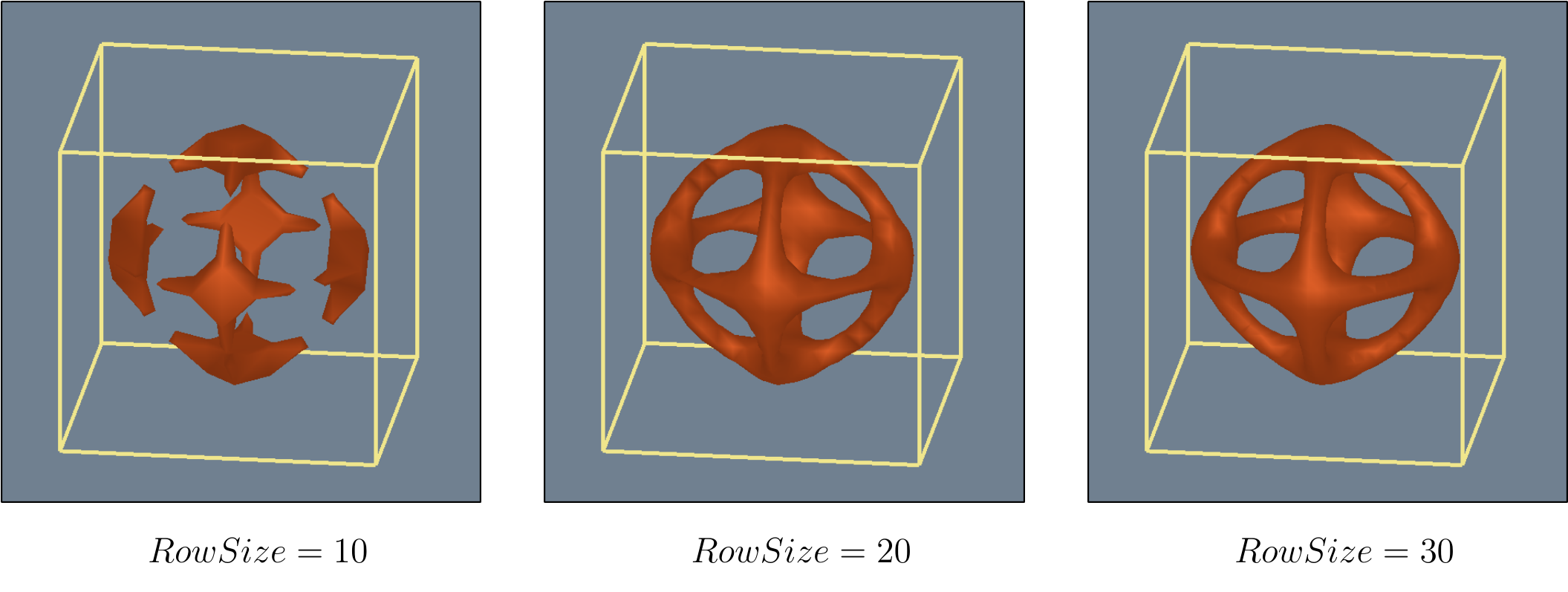
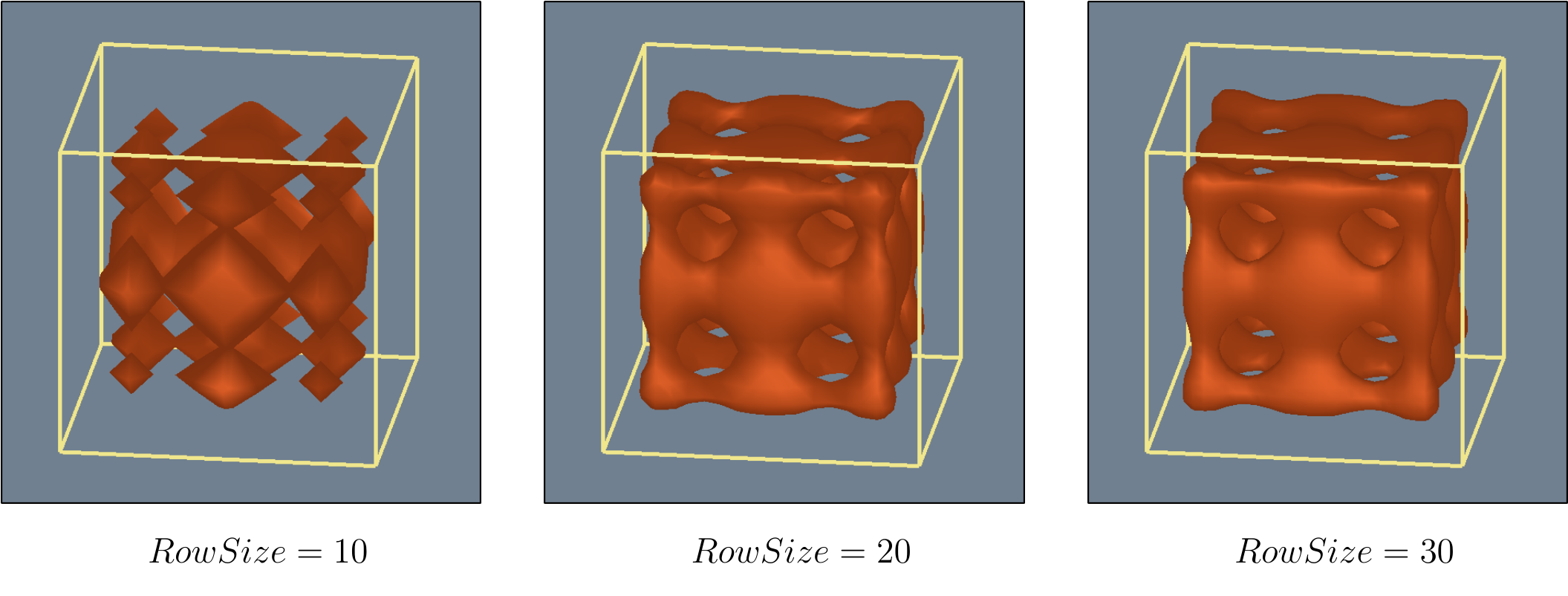
The Marching Cubes algorithm has a resolution. Our data set could be divided several times, increasing or decreasing the quality of a generated image, impacting computation time positively or negatively. The pictures below represent a Sphere in the middle of the working area, the borders of that area limiting our computation and representing the limits of the data set. The size is the number of cells in the grid row.
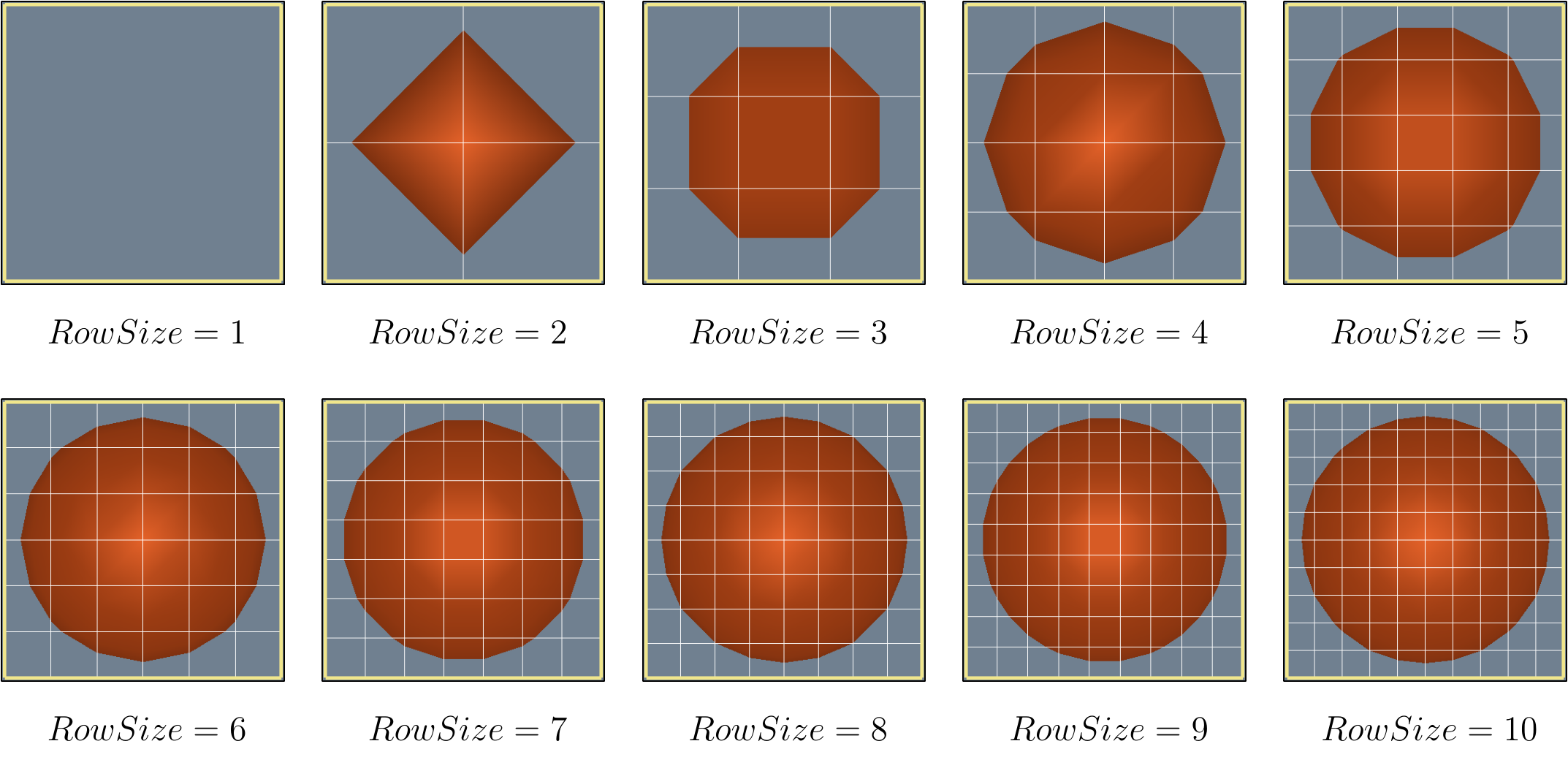
At the top of our execution, lies a simple iterator through the entire grid. We will compute cube-surface intersection for each cell in a grid.

The core of the Marching Cubes algorithm is the 256 ways a surface can intersect the cube. Although, there are only 14 possible intersection cases which could be rotated and mirrored to fulfil all 256 surface intersection variants, the better approach is to use precalculated lookup-up tables with the triangulation of all possible scenarios.
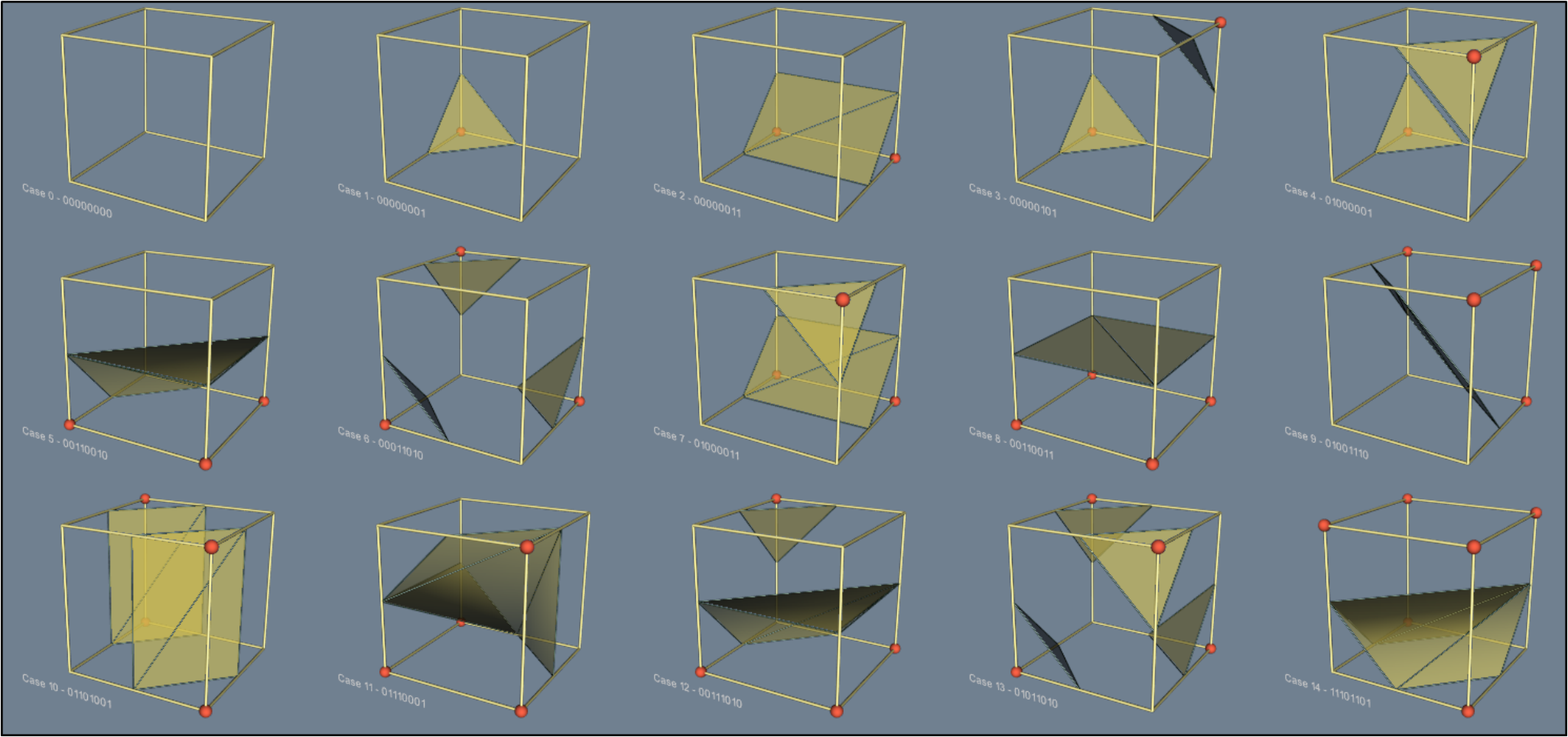
To implement the Marching Cubes algorithm, we need the following lookup tables (I’ve taken them from Paul Bourke’s website):
The list of the edges intersected by the surface for all $256$ possible vertex states. For each entry in the table, if edge $N$ is intersected, then bit $N$ is set to $1$, otherwise $0$. The picture above shows the edge numbering.
// For any edge, if one vertex is inside the surface and the other is outside the surface then the edge intersects the surface
// For each of the 8 vertices of the cube can be two possible states: either inside or outside the surface
// For any cube, there are 2^8=256 possible sets of vertex states
// This table lists the edges intersected by the surface for all 256 possible vertex states
// There are 12 edges. For each entry in the table, if edge #n is intersected, then bit #n is set to 1
const GLint CubeEdgeFlags[256] = {
0x000, 0x109, 0x203, 0x30a, 0x406, 0x50f, 0x605, 0x70c, 0x80c, 0x905, 0xa0f, 0xb06, 0xc0a, 0xd03, 0xe09, 0xf00,
0x190, 0x099, 0x393, 0x29a, 0x596, 0x49f, 0x795, 0x69c, 0x99c, 0x895, 0xb9f, 0xa96, 0xd9a, 0xc93, 0xf99, 0xe90,
0x230, 0x339, 0x033, 0x13a, 0x636, 0x73f, 0x435, 0x53c, 0xa3c, 0xb35, 0x83f, 0x936, 0xe3a, 0xf33, 0xc39, 0xd30,
0x3a0, 0x2a9, 0x1a3, 0x0aa, 0x7a6, 0x6af, 0x5a5, 0x4ac, 0xbac, 0xaa5, 0x9af, 0x8a6, 0xfaa, 0xea3, 0xda9, 0xca0,
0x460, 0x569, 0x663, 0x76a, 0x066, 0x16f, 0x265, 0x36c, 0xc6c, 0xd65, 0xe6f, 0xf66, 0x86a, 0x963, 0xa69, 0xb60,
0x5f0, 0x4f9, 0x7f3, 0x6fa, 0x1f6, 0x0ff, 0x3f5, 0x2fc, 0xdfc, 0xcf5, 0xfff, 0xef6, 0x9fa, 0x8f3, 0xbf9, 0xaf0,
0x650, 0x759, 0x453, 0x55a, 0x256, 0x35f, 0x055, 0x15c, 0xe5c, 0xf55, 0xc5f, 0xd56, 0xa5a, 0xb53, 0x859, 0x950,
0x7c0, 0x6c9, 0x5c3, 0x4ca, 0x3c6, 0x2cf, 0x1c5, 0x0cc, 0xfcc, 0xec5, 0xdcf, 0xcc6, 0xbca, 0xac3, 0x9c9, 0x8c0,
0x8c0, 0x9c9, 0xac3, 0xbca, 0xcc6, 0xdcf, 0xec5, 0xfcc, 0x0cc, 0x1c5, 0x2cf, 0x3c6, 0x4ca, 0x5c3, 0x6c9, 0x7c0,
0x950, 0x859, 0xb53, 0xa5a, 0xd56, 0xc5f, 0xf55, 0xe5c, 0x15c, 0x055, 0x35f, 0x256, 0x55a, 0x453, 0x759, 0x650,
0xaf0, 0xbf9, 0x8f3, 0x9fa, 0xef6, 0xfff, 0xcf5, 0xdfc, 0x2fc, 0x3f5, 0x0ff, 0x1f6, 0x6fa, 0x7f3, 0x4f9, 0x5f0,
0xb60, 0xa69, 0x963, 0x86a, 0xf66, 0xe6f, 0xd65, 0xc6c, 0x36c, 0x265, 0x16f, 0x066, 0x76a, 0x663, 0x569, 0x460,
0xca0, 0xda9, 0xea3, 0xfaa, 0x8a6, 0x9af, 0xaa5, 0xbac, 0x4ac, 0x5a5, 0x6af, 0x7a6, 0x0aa, 0x1a3, 0x2a9, 0x3a0,
0xd30, 0xc39, 0xf33, 0xe3a, 0x936, 0x83f, 0xb35, 0xa3c, 0x53c, 0x435, 0x73f, 0x636, 0x13a, 0x033, 0x339, 0x230,
0xe90, 0xf99, 0xc93, 0xd9a, 0xa96, 0xb9f, 0x895, 0x99c, 0x69c, 0x795, 0x49f, 0x596, 0x29a, 0x393, 0x099, 0x190,
0xf00, 0xe09, 0xd03, 0xc0a, 0xb06, 0xa0f, 0x905, 0x80c, 0x70c, 0x605, 0x50f, 0x406, 0x30a, 0x203, 0x109, 0x000
};
For each of the possible vertex states listed in CubeEdgeFlags there is a specific triangulation of the edge intersection points. TriangleConnectionTable lists all of them in the form triples. $-1$ is invalid value.
// For each of the possible vertex states listed in CubeEdgeFlags there is a specific triangulation of the edge intersection
// points. TriangleConnectionTable lists all of them in the form of 0-5 edge triples with the list terminated by the invalid
// value -1.
//
// For example:
// TriangleConnectionTable[3] list the 2 triangles formed when corner[0] and corner[1] are inside of the surface,
// but the rest of the cube is not .
static const GLint TriangleConnectionTable[256][16] = {
{-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 0, 8, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 0, 1, 9, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 1, 8, 3, 9, 8, 1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 1, 2, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 0, 8, 3, 1, 2, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 9, 2, 10, 0, 2, 9, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 2, 8, 3, 2, 10, 8, 10, 9, 8, -1, -1, -1, -1, -1, -1, -1},
{ 3, 11, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 0, 11, 2, 8, 11, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 1, 9, 0, 2, 3, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 1, 11, 2, 1, 9, 11, 9, 8, 11, -1, -1, -1, -1, -1, -1, -1},
{ 3, 10, 1, 11, 10, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 0, 10, 1, 0, 8, 10, 8, 11, 10, -1, -1, -1, -1, -1, -1, -1},
{ 3, 9, 0, 3, 11, 9, 11, 10, 9, -1, -1, -1, -1, -1, -1, -1},
{ 9, 8, 10, 10, 8, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 4, 7, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 4, 3, 0, 7, 3, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 0, 1, 9, 8, 4, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 4, 1, 9, 4, 7, 1, 7, 3, 1, -1, -1, -1, -1, -1, -1, -1},
{ 1, 2, 10, 8, 4, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 3, 4, 7, 3, 0, 4, 1, 2, 10, -1, -1, -1, -1, -1, -1, -1},
{ 9, 2, 10, 9, 0, 2, 8, 4, 7, -1, -1, -1, -1, -1, -1, -1},
{ 2, 10, 9, 2, 9, 7, 2, 7, 3, 7, 9, 4, -1, -1, -1, -1},
{ 8, 4, 7, 3, 11, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{11, 4, 7, 11, 2, 4, 2, 0, 4, -1, -1, -1, -1, -1, -1, -1},
{ 9, 0, 1, 8, 4, 7, 2, 3, 11, -1, -1, -1, -1, -1, -1, -1},
{ 4, 7, 11, 9, 4, 11, 9, 11, 2, 9, 2, 1, -1, -1, -1, -1},
{ 3, 10, 1, 3, 11, 10, 7, 8, 4, -1, -1, -1, -1, -1, -1, -1},
{ 1, 11, 10, 1, 4, 11, 1, 0, 4, 7, 11, 4, -1, -1, -1, -1},
{ 4, 7, 8, 9, 0, 11, 9, 11, 10, 11, 0, 3, -1, -1, -1, -1},
{ 4, 7, 11, 4, 11, 9, 9, 11, 10, -1, -1, -1, -1, -1, -1, -1},
{ 9, 5, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 9, 5, 4, 0, 8, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 0, 5, 4, 1, 5, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 8, 5, 4, 8, 3, 5, 3, 1, 5, -1, -1, -1, -1, -1, -1, -1},
{ 1, 2, 10, 9, 5, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 3, 0, 8, 1, 2, 10, 4, 9, 5, -1, -1, -1, -1, -1, -1, -1},
{ 5, 2, 10, 5, 4, 2, 4, 0, 2, -1, -1, -1, -1, -1, -1, -1},
{ 2, 10, 5, 3, 2, 5, 3, 5, 4, 3, 4, 8, -1, -1, -1, -1},
{ 9, 5, 4, 2, 3, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 0, 11, 2, 0, 8, 11, 4, 9, 5, -1, -1, -1, -1, -1, -1, -1},
{ 0, 5, 4, 0, 1, 5, 2, 3, 11, -1, -1, -1, -1, -1, -1, -1},
{ 2, 1, 5, 2, 5, 8, 2, 8, 11, 4, 8, 5, -1, -1, -1, -1},
{10, 3, 11, 10, 1, 3, 9, 5, 4, -1, -1, -1, -1, -1, -1, -1},
{ 4, 9, 5, 0, 8, 1, 8, 10, 1, 8, 11, 10, -1, -1, -1, -1},
{ 5, 4, 0, 5, 0, 11, 5, 11, 10, 11, 0, 3, -1, -1, -1, -1},
{ 5, 4, 8, 5, 8, 10, 10, 8, 11, -1, -1, -1, -1, -1, -1, -1},
{ 9, 7, 8, 5, 7, 9, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 9, 3, 0, 9, 5, 3, 5, 7, 3, -1, -1, -1, -1, -1, -1, -1},
{ 0, 7, 8, 0, 1, 7, 1, 5, 7, -1, -1, -1, -1, -1, -1, -1},
{ 1, 5, 3, 3, 5, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 9, 7, 8, 9, 5, 7, 10, 1, 2, -1, -1, -1, -1, -1, -1, -1},
{10, 1, 2, 9, 5, 0, 5, 3, 0, 5, 7, 3, -1, -1, -1, -1},
{ 8, 0, 2, 8, 2, 5, 8, 5, 7, 10, 5, 2, -1, -1, -1, -1},
{ 2, 10, 5, 2, 5, 3, 3, 5, 7, -1, -1, -1, -1, -1, -1, -1},
{ 7, 9, 5, 7, 8, 9, 3, 11, 2, -1, -1, -1, -1, -1, -1, -1},
{ 9, 5, 7, 9, 7, 2, 9, 2, 0, 2, 7, 11, -1, -1, -1, -1},
{ 2, 3, 11, 0, 1, 8, 1, 7, 8, 1, 5, 7, -1, -1, -1, -1},
{11, 2, 1, 11, 1, 7, 7, 1, 5, -1, -1, -1, -1, -1, -1, -1},
{ 9, 5, 8, 8, 5, 7, 10, 1, 3, 10, 3, 11, -1, -1, -1, -1},
{ 5, 7, 0, 5, 0, 9, 7, 11, 0, 1, 0, 10, 11, 10, 0, -1},
{11, 10, 0, 11, 0, 3, 10, 5, 0, 8, 0, 7, 5, 7, 0, -1},
{11, 10, 5, 7, 11, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{10, 6, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 0, 8, 3, 5, 10, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 9, 0, 1, 5, 10, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 1, 8, 3, 1, 9, 8, 5, 10, 6, -1, -1, -1, -1, -1, -1, -1},
{ 1, 6, 5, 2, 6, 1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 1, 6, 5, 1, 2, 6, 3, 0, 8, -1, -1, -1, -1, -1, -1, -1},
{ 9, 6, 5, 9, 0, 6, 0, 2, 6, -1, -1, -1, -1, -1, -1, -1},
{ 5, 9, 8, 5, 8, 2, 5, 2, 6, 3, 2, 8, -1, -1, -1, -1},
{ 2, 3, 11, 10, 6, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{11, 0, 8, 11, 2, 0, 10, 6, 5, -1, -1, -1, -1, -1, -1, -1},
{ 0, 1, 9, 2, 3, 11, 5, 10, 6, -1, -1, -1, -1, -1, -1, -1},
{ 5, 10, 6, 1, 9, 2, 9, 11, 2, 9, 8, 11, -1, -1, -1, -1},
{ 6, 3, 11, 6, 5, 3, 5, 1, 3, -1, -1, -1, -1, -1, -1, -1},
{ 0, 8, 11, 0, 11, 5, 0, 5, 1, 5, 11, 6, -1, -1, -1, -1},
{ 3, 11, 6, 0, 3, 6, 0, 6, 5, 0, 5, 9, -1, -1, -1, -1},
{ 6, 5, 9, 6, 9, 11, 11, 9, 8, -1, -1, -1, -1, -1, -1, -1},
{ 5, 10, 6, 4, 7, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 4, 3, 0, 4, 7, 3, 6, 5, 10, -1, -1, -1, -1, -1, -1, -1},
{ 1, 9, 0, 5, 10, 6, 8, 4, 7, -1, -1, -1, -1, -1, -1, -1},
{10, 6, 5, 1, 9, 7, 1, 7, 3, 7, 9, 4, -1, -1, -1, -1},
{ 6, 1, 2, 6, 5, 1, 4, 7, 8, -1, -1, -1, -1, -1, -1, -1},
{ 1, 2, 5, 5, 2, 6, 3, 0, 4, 3, 4, 7, -1, -1, -1, -1},
{ 8, 4, 7, 9, 0, 5, 0, 6, 5, 0, 2, 6, -1, -1, -1, -1},
{ 7, 3, 9, 7, 9, 4, 3, 2, 9, 5, 9, 6, 2, 6, 9, -1},
{ 3, 11, 2, 7, 8, 4, 10, 6, 5, -1, -1, -1, -1, -1, -1, -1},
{ 5, 10, 6, 4, 7, 2, 4, 2, 0, 2, 7, 11, -1, -1, -1, -1},
{ 0, 1, 9, 4, 7, 8, 2, 3, 11, 5, 10, 6, -1, -1, -1, -1},
{ 9, 2, 1, 9, 11, 2, 9, 4, 11, 7, 11, 4, 5, 10, 6, -1},
{ 8, 4, 7, 3, 11, 5, 3, 5, 1, 5, 11, 6, -1, -1, -1, -1},
{ 5, 1, 11, 5, 11, 6, 1, 0, 11, 7, 11, 4, 0, 4, 11, -1},
{ 0, 5, 9, 0, 6, 5, 0, 3, 6, 11, 6, 3, 8, 4, 7, -1},
{ 6, 5, 9, 6, 9, 11, 4, 7, 9, 7, 11, 9, -1, -1, -1, -1},
{10, 4, 9, 6, 4, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 4, 10, 6, 4, 9, 10, 0, 8, 3, -1, -1, -1, -1, -1, -1, -1},
{10, 0, 1, 10, 6, 0, 6, 4, 0, -1, -1, -1, -1, -1, -1, -1},
{ 8, 3, 1, 8, 1, 6, 8, 6, 4, 6, 1, 10, -1, -1, -1, -1},
{ 1, 4, 9, 1, 2, 4, 2, 6, 4, -1, -1, -1, -1, -1, -1, -1},
{ 3, 0, 8, 1, 2, 9, 2, 4, 9, 2, 6, 4, -1, -1, -1, -1},
{ 0, 2, 4, 4, 2, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 8, 3, 2, 8, 2, 4, 4, 2, 6, -1, -1, -1, -1, -1, -1, -1},
{10, 4, 9, 10, 6, 4, 11, 2, 3, -1, -1, -1, -1, -1, -1, -1},
{ 0, 8, 2, 2, 8, 11, 4, 9, 10, 4, 10, 6, -1, -1, -1, -1},
{ 3, 11, 2, 0, 1, 6, 0, 6, 4, 6, 1, 10, -1, -1, -1, -1},
{ 6, 4, 1, 6, 1, 10, 4, 8, 1, 2, 1, 11, 8, 11, 1, -1},
{ 9, 6, 4, 9, 3, 6, 9, 1, 3, 11, 6, 3, -1, -1, -1, -1},
{ 8, 11, 1, 8, 1, 0, 11, 6, 1, 9, 1, 4, 6, 4, 1, -1},
{ 3, 11, 6, 3, 6, 0, 0, 6, 4, -1, -1, -1, -1, -1, -1, -1},
{ 6, 4, 8, 11, 6, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 7, 10, 6, 7, 8, 10, 8, 9, 10, -1, -1, -1, -1, -1, -1, -1},
{ 0, 7, 3, 0, 10, 7, 0, 9, 10, 6, 7, 10, -1, -1, -1, -1},
{10, 6, 7, 1, 10, 7, 1, 7, 8, 1, 8, 0, -1, -1, -1, -1},
{10, 6, 7, 10, 7, 1, 1, 7, 3, -1, -1, -1, -1, -1, -1, -1},
{ 1, 2, 6, 1, 6, 8, 1, 8, 9, 8, 6, 7, -1, -1, -1, -1},
{ 2, 6, 9, 2, 9, 1, 6, 7, 9, 0, 9, 3, 7, 3, 9, -1},
{ 7, 8, 0, 7, 0, 6, 6, 0, 2, -1, -1, -1, -1, -1, -1, -1},
{ 7, 3, 2, 6, 7, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 2, 3, 11, 10, 6, 8, 10, 8, 9, 8, 6, 7, -1, -1, -1, -1},
{ 2, 0, 7, 2, 7, 11, 0, 9, 7, 6, 7, 10, 9, 10, 7, -1},
{ 1, 8, 0, 1, 7, 8, 1, 10, 7, 6, 7, 10, 2, 3, 11, -1},
{11, 2, 1, 11, 1, 7, 10, 6, 1, 6, 7, 1, -1, -1, -1, -1},
{ 8, 9, 6, 8, 6, 7, 9, 1, 6, 11, 6, 3, 1, 3, 6, -1},
{ 0, 9, 1, 11, 6, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 7, 8, 0, 7, 0, 6, 3, 11, 0, 11, 6, 0, -1, -1, -1, -1},
{ 7, 11, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 7, 6, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 3, 0, 8, 11, 7, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 0, 1, 9, 11, 7, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 8, 1, 9, 8, 3, 1, 11, 7, 6, -1, -1, -1, -1, -1, -1, -1},
{10, 1, 2, 6, 11, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 1, 2, 10, 3, 0, 8, 6, 11, 7, -1, -1, -1, -1, -1, -1, -1},
{ 2, 9, 0, 2, 10, 9, 6, 11, 7, -1, -1, -1, -1, -1, -1, -1},
{ 6, 11, 7, 2, 10, 3, 10, 8, 3, 10, 9, 8, -1, -1, -1, -1},
{ 7, 2, 3, 6, 2, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 7, 0, 8, 7, 6, 0, 6, 2, 0, -1, -1, -1, -1, -1, -1, -1},
{ 2, 7, 6, 2, 3, 7, 0, 1, 9, -1, -1, -1, -1, -1, -1, -1},
{ 1, 6, 2, 1, 8, 6, 1, 9, 8, 8, 7, 6, -1, -1, -1, -1},
{10, 7, 6, 10, 1, 7, 1, 3, 7, -1, -1, -1, -1, -1, -1, -1},
{10, 7, 6, 1, 7, 10, 1, 8, 7, 1, 0, 8, -1, -1, -1, -1},
{ 0, 3, 7, 0, 7, 10, 0, 10, 9, 6, 10, 7, -1, -1, -1, -1},
{ 7, 6, 10, 7, 10, 8, 8, 10, 9, -1, -1, -1, -1, -1, -1, -1},
{ 6, 8, 4, 11, 8, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 3, 6, 11, 3, 0, 6, 0, 4, 6, -1, -1, -1, -1, -1, -1, -1},
{ 8, 6, 11, 8, 4, 6, 9, 0, 1, -1, -1, -1, -1, -1, -1, -1},
{ 9, 4, 6, 9, 6, 3, 9, 3, 1, 11, 3, 6, -1, -1, -1, -1},
{ 6, 8, 4, 6, 11, 8, 2, 10, 1, -1, -1, -1, -1, -1, -1, -1},
{ 1, 2, 10, 3, 0, 11, 0, 6, 11, 0, 4, 6, -1, -1, -1, -1},
{ 4, 11, 8, 4, 6, 11, 0, 2, 9, 2, 10, 9, -1, -1, -1, -1},
{10, 9, 3, 10, 3, 2, 9, 4, 3, 11, 3, 6, 4, 6, 3, -1},
{ 8, 2, 3, 8, 4, 2, 4, 6, 2, -1, -1, -1, -1, -1, -1, -1},
{ 0, 4, 2, 4, 6, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 1, 9, 0, 2, 3, 4, 2, 4, 6, 4, 3, 8, -1, -1, -1, -1},
{ 1, 9, 4, 1, 4, 2, 2, 4, 6, -1, -1, -1, -1, -1, -1, -1},
{ 8, 1, 3, 8, 6, 1, 8, 4, 6, 6, 10, 1, -1, -1, -1, -1},
{10, 1, 0, 10, 0, 6, 6, 0, 4, -1, -1, -1, -1, -1, -1, -1},
{ 4, 6, 3, 4, 3, 8, 6, 10, 3, 0, 3, 9, 10, 9, 3, -1},
{10, 9, 4, 6, 10, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 4, 9, 5, 7, 6, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 0, 8, 3, 4, 9, 5, 11, 7, 6, -1, -1, -1, -1, -1, -1, -1},
{ 5, 0, 1, 5, 4, 0, 7, 6, 11, -1, -1, -1, -1, -1, -1, -1},
{11, 7, 6, 8, 3, 4, 3, 5, 4, 3, 1, 5, -1, -1, -1, -1},
{ 9, 5, 4, 10, 1, 2, 7, 6, 11, -1, -1, -1, -1, -1, -1, -1},
{ 6, 11, 7, 1, 2, 10, 0, 8, 3, 4, 9, 5, -1, -1, -1, -1},
{ 7, 6, 11, 5, 4, 10, 4, 2, 10, 4, 0, 2, -1, -1, -1, -1},
{ 3, 4, 8, 3, 5, 4, 3, 2, 5, 10, 5, 2, 11, 7, 6, -1},
{ 7, 2, 3, 7, 6, 2, 5, 4, 9, -1, -1, -1, -1, -1, -1, -1},
{ 9, 5, 4, 0, 8, 6, 0, 6, 2, 6, 8, 7, -1, -1, -1, -1},
{ 3, 6, 2, 3, 7, 6, 1, 5, 0, 5, 4, 0, -1, -1, -1, -1},
{ 6, 2, 8, 6, 8, 7, 2, 1, 8, 4, 8, 5, 1, 5, 8, -1},
{ 9, 5, 4, 10, 1, 6, 1, 7, 6, 1, 3, 7, -1, -1, -1, -1},
{ 1, 6, 10, 1, 7, 6, 1, 0, 7, 8, 7, 0, 9, 5, 4, -1},
{ 4, 0, 10, 4, 10, 5, 0, 3, 10, 6, 10, 7, 3, 7, 10, -1},
{ 7, 6, 10, 7, 10, 8, 5, 4, 10, 4, 8, 10, -1, -1, -1, -1},
{ 6, 9, 5, 6, 11, 9, 11, 8, 9, -1, -1, -1, -1, -1, -1, -1},
{ 3, 6, 11, 0, 6, 3, 0, 5, 6, 0, 9, 5, -1, -1, -1, -1},
{ 0, 11, 8, 0, 5, 11, 0, 1, 5, 5, 6, 11, -1, -1, -1, -1},
{ 6, 11, 3, 6, 3, 5, 5, 3, 1, -1, -1, -1, -1, -1, -1, -1},
{ 1, 2, 10, 9, 5, 11, 9, 11, 8, 11, 5, 6, -1, -1, -1, -1},
{ 0, 11, 3, 0, 6, 11, 0, 9, 6, 5, 6, 9, 1, 2, 10, -1},
{11, 8, 5, 11, 5, 6, 8, 0, 5, 10, 5, 2, 0, 2, 5, -1},
{ 6, 11, 3, 6, 3, 5, 2, 10, 3, 10, 5, 3, -1, -1, -1, -1},
{ 5, 8, 9, 5, 2, 8, 5, 6, 2, 3, 8, 2, -1, -1, -1, -1},
{ 9, 5, 6, 9, 6, 0, 0, 6, 2, -1, -1, -1, -1, -1, -1, -1},
{ 1, 5, 8, 1, 8, 0, 5, 6, 8, 3, 8, 2, 6, 2, 8, -1},
{ 1, 5, 6, 2, 1, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 1, 3, 6, 1, 6, 10, 3, 8, 6, 5, 6, 9, 8, 9, 6, -1},
{10, 1, 0, 10, 0, 6, 9, 5, 0, 5, 6, 0, -1, -1, -1, -1},
{ 0, 3, 8, 5, 6, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{10, 5, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{11, 5, 10, 7, 5, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{11, 5, 10, 11, 7, 5, 8, 3, 0, -1, -1, -1, -1, -1, -1, -1},
{ 5, 11, 7, 5, 10, 11, 1, 9, 0, -1, -1, -1, -1, -1, -1, -1},
{10, 7, 5, 10, 11, 7, 9, 8, 1, 8, 3, 1, -1, -1, -1, -1},
{11, 1, 2, 11, 7, 1, 7, 5, 1, -1, -1, -1, -1, -1, -1, -1},
{ 0, 8, 3, 1, 2, 7, 1, 7, 5, 7, 2, 11, -1, -1, -1, -1},
{ 9, 7, 5, 9, 2, 7, 9, 0, 2, 2, 11, 7, -1, -1, -1, -1},
{ 7, 5, 2, 7, 2, 11, 5, 9, 2, 3, 2, 8, 9, 8, 2, -1},
{ 2, 5, 10, 2, 3, 5, 3, 7, 5, -1, -1, -1, -1, -1, -1, -1},
{ 8, 2, 0, 8, 5, 2, 8, 7, 5, 10, 2, 5, -1, -1, -1, -1},
{ 9, 0, 1, 5, 10, 3, 5, 3, 7, 3, 10, 2, -1, -1, -1, -1},
{ 9, 8, 2, 9, 2, 1, 8, 7, 2, 10, 2, 5, 7, 5, 2, -1},
{ 1, 3, 5, 3, 7, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 0, 8, 7, 0, 7, 1, 1, 7, 5, -1, -1, -1, -1, -1, -1, -1},
{ 9, 0, 3, 9, 3, 5, 5, 3, 7, -1, -1, -1, -1, -1, -1, -1},
{ 9, 8, 7, 5, 9, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 5, 8, 4, 5, 10, 8, 10, 11, 8, -1, -1, -1, -1, -1, -1, -1},
{ 5, 0, 4, 5, 11, 0, 5, 10, 11, 11, 3, 0, -1, -1, -1, -1},
{ 0, 1, 9, 8, 4, 10, 8, 10, 11, 10, 4, 5, -1, -1, -1, -1},
{10, 11, 4, 10, 4, 5, 11, 3, 4, 9, 4, 1, 3, 1, 4, -1},
{ 2, 5, 1, 2, 8, 5, 2, 11, 8, 4, 5, 8, -1, -1, -1, -1},
{ 0, 4, 11, 0, 11, 3, 4, 5, 11, 2, 11, 1, 5, 1, 11, -1},
{ 0, 2, 5, 0, 5, 9, 2, 11, 5, 4, 5, 8, 11, 8, 5, -1},
{ 9, 4, 5, 2, 11, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 2, 5, 10, 3, 5, 2, 3, 4, 5, 3, 8, 4, -1, -1, -1, -1},
{ 5, 10, 2, 5, 2, 4, 4, 2, 0, -1, -1, -1, -1, -1, -1, -1},
{ 3, 10, 2, 3, 5, 10, 3, 8, 5, 4, 5, 8, 0, 1, 9, -1},
{ 5, 10, 2, 5, 2, 4, 1, 9, 2, 9, 4, 2, -1, -1, -1, -1},
{ 8, 4, 5, 8, 5, 3, 3, 5, 1, -1, -1, -1, -1, -1, -1, -1},
{ 0, 4, 5, 1, 0, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 8, 4, 5, 8, 5, 3, 9, 0, 5, 0, 3, 5, -1, -1, -1, -1},
{ 9, 4, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 4, 11, 7, 4, 9, 11, 9, 10, 11, -1, -1, -1, -1, -1, -1, -1},
{ 0, 8, 3, 4, 9, 7, 9, 11, 7, 9, 10, 11, -1, -1, -1, -1},
{ 1, 10, 11, 1, 11, 4, 1, 4, 0, 7, 4, 11, -1, -1, -1, -1},
{ 3, 1, 4, 3, 4, 8, 1, 10, 4, 7, 4, 11, 10, 11, 4, -1},
{ 4, 11, 7, 9, 11, 4, 9, 2, 11, 9, 1, 2, -1, -1, -1, -1},
{ 9, 7, 4, 9, 11, 7, 9, 1, 11, 2, 11, 1, 0, 8, 3, -1},
{11, 7, 4, 11, 4, 2, 2, 4, 0, -1, -1, -1, -1, -1, -1, -1},
{11, 7, 4, 11, 4, 2, 8, 3, 4, 3, 2, 4, -1, -1, -1, -1},
{ 2, 9, 10, 2, 7, 9, 2, 3, 7, 7, 4, 9, -1, -1, -1, -1},
{ 9, 10, 7, 9, 7, 4, 10, 2, 7, 8, 7, 0, 2, 0, 7, -1},
{ 3, 7, 10, 3, 10, 2, 7, 4, 10, 1, 10, 0, 4, 0, 10, -1},
{ 1, 10, 2, 8, 7, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 4, 9, 1, 4, 1, 7, 7, 1, 3, -1, -1, -1, -1, -1, -1, -1},
{ 4, 9, 1, 4, 1, 7, 0, 8, 1, 8, 7, 1, -1, -1, -1, -1},
{ 4, 0, 3, 7, 4, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 4, 8, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 9, 10, 8, 10, 11, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 3, 0, 9, 3, 9, 11, 11, 9, 10, -1, -1, -1, -1, -1, -1, -1},
{ 0, 1, 10, 0, 10, 8, 8, 10, 11, -1, -1, -1, -1, -1, -1, -1},
{ 3, 1, 10, 11, 3, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 1, 2, 11, 1, 11, 9, 9, 11, 8, -1, -1, -1, -1, -1, -1, -1},
{ 3, 0, 9, 3, 9, 11, 1, 2, 9, 2, 11, 9, -1, -1, -1, -1},
{ 0, 2, 11, 8, 0, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 3, 2, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 2, 3, 8, 2, 8, 10, 10, 8, 9, -1, -1, -1, -1, -1, -1, -1},
{ 9, 10, 2, 0, 9, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 2, 3, 8, 2, 8, 10, 0, 1, 8, 1, 10, 8, -1, -1, -1, -1},
{ 1, 10, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 1, 3, 8, 9, 1, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 0, 9, 1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{ 0, 3, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1}
};
VertexOffset table lists the positions, relative to vertex0, of each of the 8 vertices of a cube. Usage of this table is optional, but it helps to reduce the amount of code.
// VertexOffset lists the positions, relative to vertex0, of each of the 8 vertices of a cube
const GLfloat VertexOffset[8][3] = {
{0.0, 0.0, 0.0},
{1.0, 0.0, 0.0},
{1.0, 1.0, 0.0},
{0.0, 1.0, 0.0},
{0.0, 0.0, 1.0},
{1.0, 0.0, 1.0},
{1.0, 1.0, 1.0},
{0.0, 1.0, 1.0}
};
EdgeConnection table lists the index of the endpoint vertices for each of the 12 edges of the cube. Usage of this table is also optional and helps to reduce the amount of code.
// EdgeConnection lists the index of the endpoint vertices for each of the 12 edges of the cube
const GLint EdgeConnection[12][2] = {
{0, 1},
{1, 2},
{2, 3},
{3, 0},
{4, 5},
{5, 6},
{6, 7},
{7, 4},
{0, 4},
{1, 5},
{2, 6},
{3, 7}
};
The algorithm iterates through the grid computing and drawing triangles for each cell.
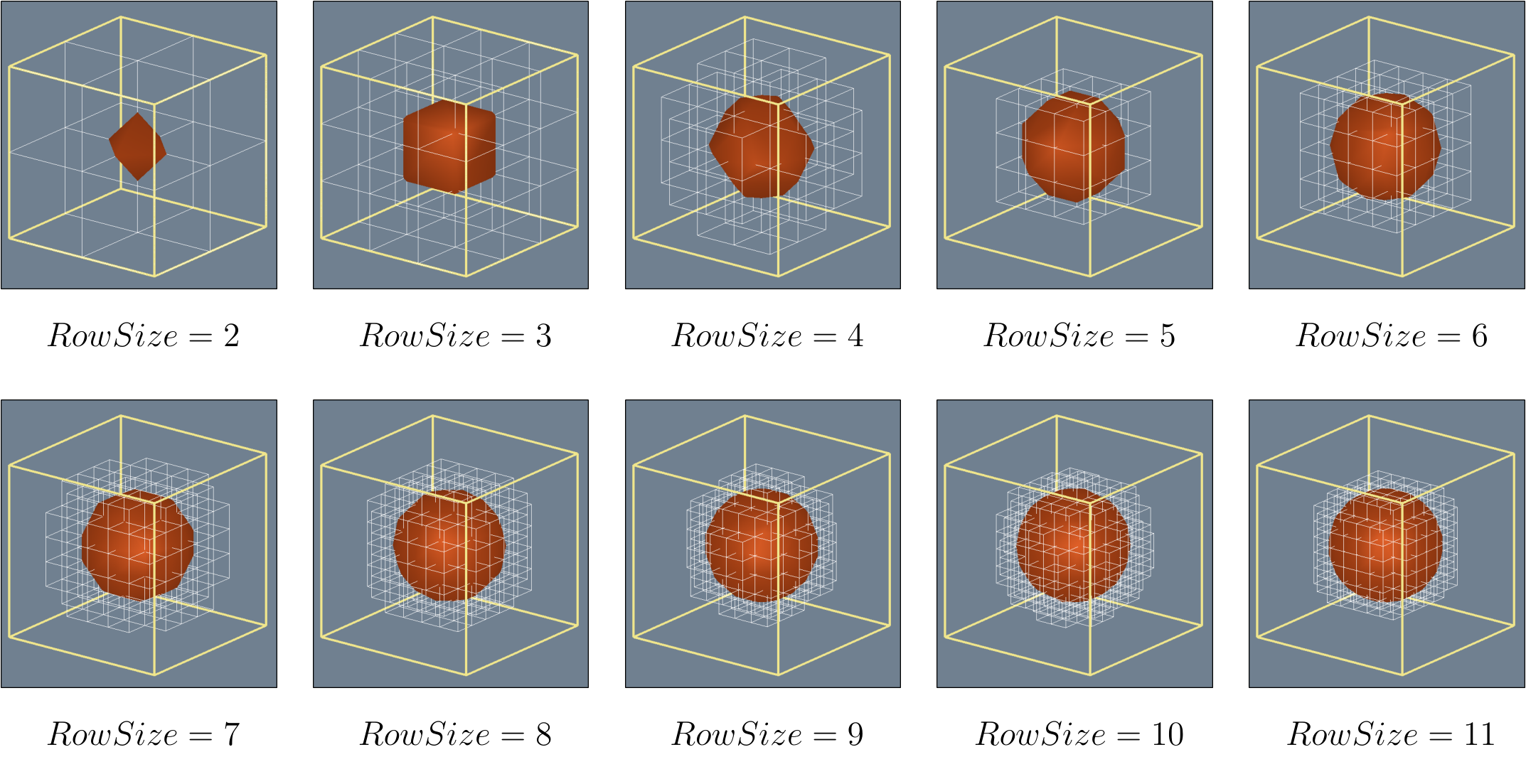
For each cell, the vertices that lie on one side of the Scalar Field are detected using the Surface Value (a.k.a. isovalue) provided by the user, which normally represents the size of the generated surface. The combination of vertices forms edge flags for a cell. The edge flag is a $12$-binary digit number, one bit for each of the $12$ edges of a cell. If the combination of edge flags for a cell is zero, such cells lie entirely inside or entirely outside the surface and should not be considered. The algorithm should skip them. CubeEdgeFlags lookup table supplies with all $256$ available edge flag combinations.
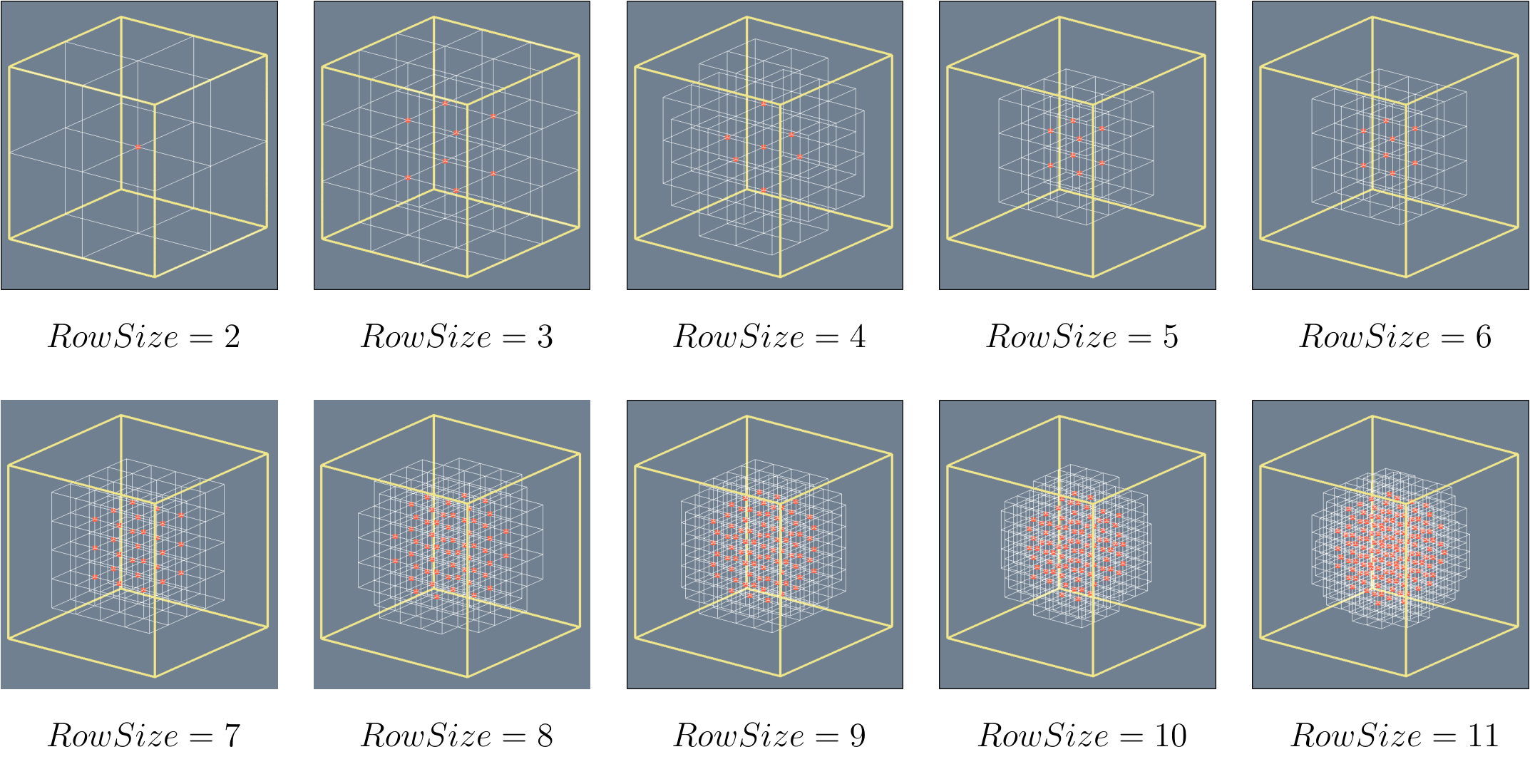
For each edge in the cell with the non-zero edge flag value, the algorithm interpolates a pair of vertices for intersecting edge to get the edge-surface intersection point using the given Surface Value. The EdgeConnection lookup table supplies the pairs of vertices for an edge. The resultant points are the vertices on the surface that will be used to draw triangles.
In the last step, the algorithm looks in the TriangleConnectionTable for triples of vertices for the edge flag combination for a cell and draws triangles using found vertices.
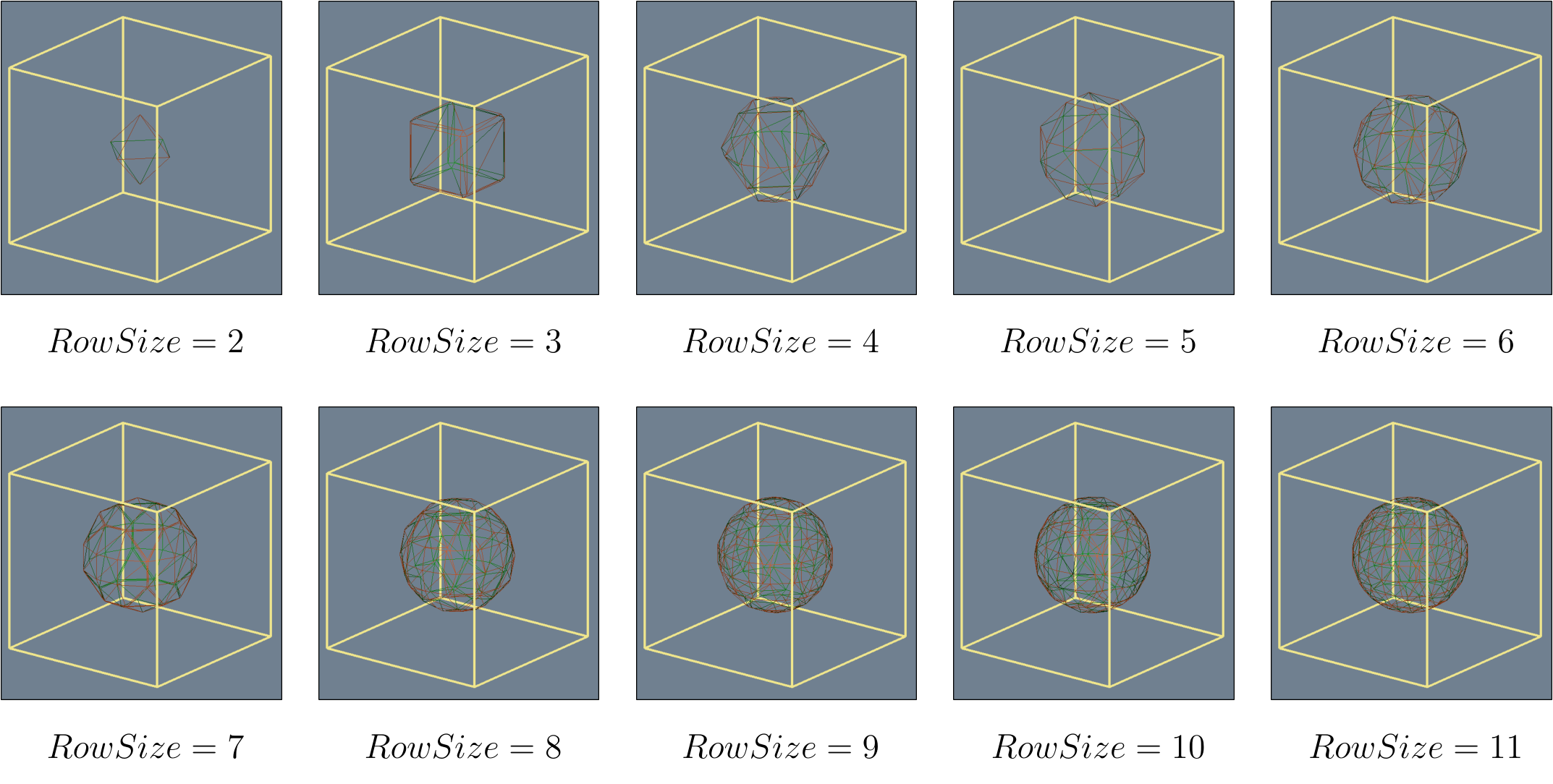
Additionally, we need a function to interpolate between two vertices to get the exact intersection point between two points of the edge.

To sum up, everything that was said, here is the pseudocode of the Marching Cubes algorithm implementation.

Paul Bourke has a perfect collection of different implementations, and I encourage you to look there for inspiration. Here I’m presenting my compilation of different ideas with my improvements.
The code below is self-sufficient, but requires linking with the GLUT library. I’ve prepared an archive with the implementation using VCPKG as dependency management, but you can just take C++ files and build them using your preferred way. Licence: MIT.
Option 1: Temporary local environment
# Assuming that VCPKG cloned and bootstrapped in ~/vcpkg
export PATH="~/vcpkg;${PATH}"
Option 2: Local environment and Bash profile
# Assuming that VCPKG cloned and bootstrapped in ~/vcpkg
export PATH="~/vcpkg;${PATH}"
echo 'export PATH="~/vcpkg;${PATH}"' >> ~/.bashrc
Important Note: the VCPKG requests installation of additional packages
build.shOption 1: Command Line tools
REM Assuming that VCPKG cloned and bootstrapped in c:\src\vcpkg
REM setx for the global environment, set for the local
setx PATH c:\src\vcpkg;%PATH%
set PATH c:\src\vcpkg;%PATH%
Option 2: PowerShell
# Assuming that VCPKG cloned and bootstrapped in c:\src\vcpkg
[Environment]::SetEnvironmentVariable("PATH", "c:\src\vcpkg;${PATH}", "Machine")
Set-Item -Path Env:PATH -Value "c:\src\vcpkg;${PATH}"
Option 3: Manualy in System Properties –> Environment Variables
build.batbuild\mcgl.sln in Visual Studio to work with the source code1 show internal grid
2 show external grid
3 show internal points in red
4 show internal points in white
5 show external points in red
6 show external points in white
PageUp/PageDown increase/decrease surface value
Shift + PageUp/PageDown increase/decrease surface value
s change sample function forward
Shift + s change sample function backward
c toggle marching cubes / marching tetrahedrons
w wireframe on/off
l toggle lighting / color-by-normal
Home spin scene on/off
Shift + Home slow spin scene on/off
End source point animation on/off
Shift + End slow source point animation on/off